|
|
|
BRAIDS
(14 May - 13 Jul 2007)
Organizing Committee
· Confirmed Visitors
· Background
· Main Theme
Activities · Membership
Application
Co-chairs
Members
(The pictures below are taken from
Mitch Berger's website, where they are discussed in more
detail.)
The notion of a braid as "anything plaited,
interwoven, or entwined" goes back many centuries, and
braids have been used universally for decoration, art and
fastening purposes. Only recently have mathematicians tried
to describe braids by means of abstract theory.
Fortuitously, as the theory has developed, it has enabled
applications to outstanding problems in physics, chemistry
and biology.
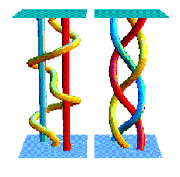 In topology, braid theory is an abstract
geometric theory studying the everyday braid concept, and
some generalizations. The idea is that braids can be
organized into groups, in which the group operation is "do
the first braid on a set of strings, and then follow it with
a second on the twisted strings". Such groups may be
described by explicit presentations, as was shown by E.
Artin in 1925. A braid with n strands can also be thought of
as paths of n distinct particles moving through time, and
which do not collide (with variations involving particles
which can collide). Braids may also be given a deeper
mathematical interpretation: as the fundamental group of
certain configuration spaces, comprising configurations of
distinct points in a manifold X. In topology, braid theory is an abstract
geometric theory studying the everyday braid concept, and
some generalizations. The idea is that braids can be
organized into groups, in which the group operation is "do
the first braid on a set of strings, and then follow it with
a second on the twisted strings". Such groups may be
described by explicit presentations, as was shown by E.
Artin in 1925. A braid with n strands can also be thought of
as paths of n distinct particles moving through time, and
which do not collide (with variations involving particles
which can collide). Braids may also be given a deeper
mathematical interpretation: as the fundamental group of
certain configuration spaces, comprising configurations of
distinct points in a manifold X.
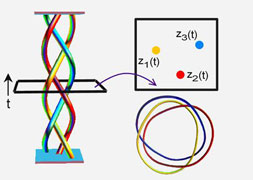 When X is the plane, the braid can be
closed, that is, corresponding ends can be connected in
pairs, to form a link, a possibly intertwined union of
possibly knotted loops in three dimensions. The number of
components of the link depends on the permutation of strands
determined by the link. J.W. Alexander (1928) observed that
every link can be obtained in this way from a braid (see
also work by Markov). Different braids can give rise to the
same link, just as different crossing diagrams can give rise
to the same knot. The Jones polynomial of a link (1987) is
defined, a priori, as a braid invariant and then shown to
depend only on the class of the closed braid. When X is the plane, the braid can be
closed, that is, corresponding ends can be connected in
pairs, to form a link, a possibly intertwined union of
possibly knotted loops in three dimensions. The number of
components of the link depends on the permutation of strands
determined by the link. J.W. Alexander (1928) observed that
every link can be obtained in this way from a braid (see
also work by Markov). Different braids can give rise to the
same link, just as different crossing diagrams can give rise
to the same knot. The Jones polynomial of a link (1987) is
defined, a priori, as a braid invariant and then shown to
depend only on the class of the closed braid.
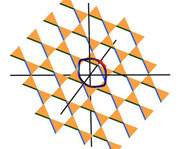 Until recently, the study of braids has
been regarded as a topic within knot theory, a major branch
of low-dimensional topology. However, work largely done at
NUS [2] has shown that the study of Brunnian braids has
application to longstanding problems in homotopy theory, and
in particular the fundamental question of the homotopy
groups of spheres. (Brunnian braids [Brunn, 1892] are those
which reduce to the trivial, untwisted braid when any strand
is removed. The familiar Borromean rings are the link
obtained by closing up one such Brunnian braid.)
Until recently, the study of braids has
been regarded as a topic within knot theory, a major branch
of low-dimensional topology. However, work largely done at
NUS [2] has shown that the study of Brunnian braids has
application to longstanding problems in homotopy theory, and
in particular the fundamental question of the homotopy
groups of spheres. (Brunnian braids [Brunn, 1892] are those
which reduce to the trivial, untwisted braid when any strand
is removed. The familiar Borromean rings are the link
obtained by closing up one such Brunnian braid.)
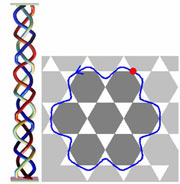 To date, most mathematical interest in
braids has come from algebraists, topologists and
mathematical physicists. As well, braids are also engaging
the attention of computer scientists, as a basis for
public-key cryptosystems. Probabilistic algorithms are being
employed to search for solutions to word problems in the
braid group. Relevance to robotics, cryptography and to magnetohydrodynamics is also to be explored during the
program.
To date, most mathematical interest in
braids has come from algebraists, topologists and
mathematical physicists. As well, braids are also engaging
the attention of computer scientists, as a basis for
public-key cryptosystems. Probabilistic algorithms are being
employed to search for solutions to word problems in the
braid group. Relevance to robotics, cryptography and to magnetohydrodynamics is also to be explored during the
program.
References:
- D. Bensimon, G. Charvin & V. Croquette: DNA
unbraiding by a single type II topoisomerase, PHYS 196
[636703],
http://www.hackberry.chem.trinity.edu/PHYS/fall2003.html
- A.J. Berrick, F.R. Cohen, Y.-L. Wong & J. Wu:
Configurations, braids and homotopy groups, J.
Amer. Math. Soc., to appear.
- C.O. Dietrich-Buchecker & J.-P. Sauvage: Interlocked and
knotted rings in biology and chemistry, in Bioorganic Chemistry Frontiers,
Springer (Berlin, 1991) Vol. 2, 195 - 248.
- D. Garber, S. Kaplan, M. Teicher, B. Tsaban and U. Vishne: Probabilistic
solutions of equations in the braid group, preprint (2004).
- R. Ghrist: Configuration spaces and braid groups on graphs in
robotics, in Braids, Links, and Mapping Class Groups: the Proceedings
of Joan Birman's 70th Birthday, AMS/IP Studies in Mathematics volume
24 (2001), 29 - 40.
- K. H. Ko, S. J. Lee, J. H. Cheon, J. W. Han, S. J. Kang and C.
S. Park, New Public-key cryptosystem using braid groups, CRYPTO 2000,
LNCS 1880 (2000), 166 - 183.
- P. Pieranski et al.: Physical Review Letters, 19 August
1996.
- P.F. Schewe & B. Stein: Braids plaited by magnetic holes,
The American Institute of Physics Bulletin of Physics News
285 (Story #2), September 9, 1996.
- Michael D. Stone, Zev Bryant, Nancy J. Crisona, Steven B. Smith,
Alexander Vologodskii, Carlos Bustamante & Nicholas R. Cozzarelli: Chirality
sensing by Escherichia coli topoisomerase IV and the mechanism of type II
topoisomerases, Proc. Nat. Acad. Sci. 100 no. 15, (July 22,
2003), 8654 - 59.
- A. V. Vologodskii, W. Zhang, V. V. Rybenkov, A. A. Podtelezhnikov,
D. Subramanian, J. D. Griffith & N. R. Cozzarelli: Mechanism of toplogy
simplification by type II DNA topoisomerases, Proc. Natl. Acad. Sci. USA
98 (2001), 3045 - 3049.
- D.M. Walba, T.C. Homan, R.M. Richards & R.C. Haltiwanger,
New J. Chem. 17 (1993), 661.
- Wikipedia,
http://www.sciencedaily.com/encyclopedia/Braid_theory
The main theme of the program is
the mathematical structure of the braid group, together with
applications arising from this structure both within
mathematics, and outside of mathematics such as (a) magnetohydrodynamics, (b) robotics and (c)
cryptography.
It is proposed to invite workers in these
different areas with the intention of cross-fertilization.
The interests of the organizers lie
mostly in topology. Therefore it is likely that most
long-term visitors will be from that area. Reflecting the
theme of the program, it is intended to have tutorials that
would:
- introduce outsiders (e.g. graduate students) to the
mathematics of braid theory
- facilitate communication between those working in
mathematical theory of braids and those who apply braids
elsewhere, specifically in magnetohydrodynamics,
robotics and cryptography.
-
PRIMA Summer School: 4 - 29
Jun 2007
jointly organized with Department of Mathematics
(PRIMA = Pacific Rim Mathematical Association)
-
Tutorials:
Week 1: 4 - 8 Jun 2007
(a) Preliminaries in topology and algebra, by E-Jay Ng: 4 hours
(b) Braids - definitions and braid groups, by Dale Rolfsen: 4 hours
Week 2: 11 - 15 Jun 2007
(a) Simplicial objects and homotopy groups, by Jie Wu: 4 hours
(b) Configuration spaces, by Fred Cohen: 2 hours
Week 3: 18 - 22 Jun 2007
(a) Magnetohydrodynamics, by Mitch Berger: 4 hours
(b) Configuration spaces and robotics, by Robert Ghrist: 2 hours
(c ) Braid groups and cryptography, by David Garber: 2 hours
- Conference:
25 - 29 Jun 2007
Confirmed Principal Speakers
M
Berger (London)
J Birman
(Columbia)
R Budney (MPIM Bonn)
F Cohen (Rochester)
David Garber (Holon Institute of Technology)
R
Ghrist (UIUC)
J
Gonzalez-Meneses (Seville)
T Kohno
(Tokyo)
D Margalit
(Utah)
L Paris
(Bourgogne)
D Rolfsen
(British Columbia)
N Wahl
(Chicago)
B
Wiest (Rennes)
We welcome contributed talks of less than 25 minutes.
Deadline for submission of abstract: 10 March 2007
Standard Registration Fee: SGD$200
Please pay by using Singapore currency at desk after
arrival, credit card and checks are not accepted.
If you seek financial support (for local expenses only),
please indicate when submitting your abstract and IMS
Membership application. Application deadline: 10 March 20074
- Public Lecture:
Title:
Robot
Swarms and the Topology of Coordination
Date & Time: 26 Jun 2007, 6.30pm - 7.30pm
Speaker:
Robert Ghrist
(University of Illinois, Urbana-Champaign)
Venue:
LT31, Block S16,
Science
Drive 1, Singapore 117543
IMS Membership is not required for participation in above
activities. For attendance at these activities,
please complete the online registration form.
If you are an IMS member or are applying for IMS
membership, you do not need to register for these activities.
The Institute for Mathematical Sciences
invites applications for membership for participation in the
above program. Limited funds to cover travel and living
expenses are available to young scientists. Applications
should be received at least three (3) months before the
commencement of membership. Application form is available in (MSWord|PDF|PS) format for download.
Membership application deadline is on the 10 March 2007.
- More information is available by writing to:
- Secretary
Institute for Mathematical Sciences
National University of Singapore
3 Prince George's Park
Singapore 118402
Republic of Singapore
- or email to imssec@nus.edu.sg.
For enquiries on scientific aspects of the program, please
email A.J. Berrick at
berrick@math.nus.edu.sg.
Organizing Committee
· Confirmed Visitors
· Background
· Main Theme
Activities · Membership
Application
|
|



